Scenario 2 for "Maze" gameplay - cooperation mode

Gameplay description

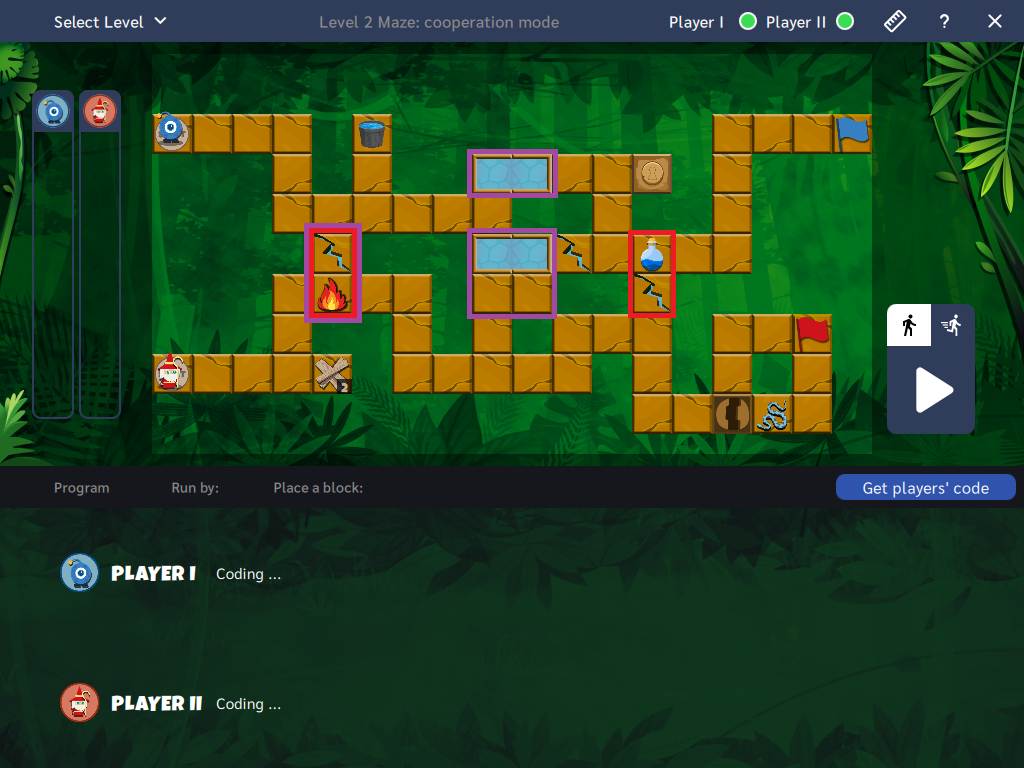
Players face the challenge of getting to the other side of the maze. The necessary condition for a correct solution is for both heroes to reach the goal at the same time. To achieve this, players must help each other and create algorithms that will complement each other and have the same length.

Example board: Board 12

The above board marks a few places on the board that are of particular importance in this mode of gameplay. A new feature in this cooperation mode is the Pass block, which allows one player to pass collected items to the other player who is on one of the adjacent fields to the first hero.

Optional places where item transfer can occur are marked in red. In one of them, the red player Elf can pass the collected wood to the blue player Kodi. In the other, the blue elixir can be passed in the opposite direction. These are suggested places, and the action itself is not required for a correct solution. In the case of planks for bridge construction, the player controlling the Elf character can build a bridge for his teammate (two possible places to use the planks are marked in purple). Using the elixir (neutralizing the blue snake) is also not necessary. However, remember that players must plan their algorithms to reach the goal fields at the same time.

Example solutions

Code for the blue player "Kodi"

The example code for the players will be presented in 2 stages for better illustration of the actions performed.

Stage 1:

Firstly, the blue player must unlock the further path for the other player. To do this, he must collect and use a bucket of water on the fire field. Be careful because the field where the player must stop is cracked, which means that you can only stand on it once. After unlocking the path for his teammate, Kodi must go to the water tanks, where using the Wait action, he will wait for the bridge to be built.

Optional actions: Kodi, instead of waiting for the bridge to be built, can build it himself if the red player had previously passed him the planks he had collected.

Stage 2:

In the second stage, the blue player, having the bridge already built, can head towards the goal, but before that happens, he must perform at least one more action. In the shown example, Kodi opens the door (required action) and collects and passes the blue elixir to the Elf. Here, note that the red player cannot collect the elixir himself due to the arrangement of the cracked fields. After performing these two actions, Kodi heads towards the goal.

Optional actions: Kodi does not have to pass the blue elixir to the other player, as the snake does not block the path. However, then the lengths of the algorithms change and the players will have to use the "Wait" actions appropriately.

Code for the red player "Elf"

Similarly to the blue player, the example code will be presented in two stages.

Stage 1:

In the first stage of the game, the red player, while waiting for the path to be unlocked by his partner, collects planks for bridge construction, and after using the Wait action, heads towards the water to build a passage for Kodi.

Optional actions: The Elf, instead of building the bridge himself, can pass the planks to the blue player. The ideal place for this action is where Kodi extinguishes the fire. The further part of the game depends on this decision.

Stage 2:

In the second stage, after building a passage for Kodi, the Elf heads to the meeting place, where the elixir for the snakes will be passed. Remember here that the Wait action must take into account not only the alignment of the algorithms but also the Pass action so that the heroes are on adjacent fields for one clock tick. After receiving the elixir, the red player heads to the goal, defeating the blue snake on the way.

Optional actions: Defeating the snake is not a required action to complete the level. If you choose a different way to reach the goal, consider the possibility of different lengths of the algorithms of both players and using the Wait action to properly align the lengths of the algorithms.